「公文式算数・数学では図形と文章問題を扱わないけど大丈夫ですか…?」と入塾面談の時に言われることがあります。
私は自信を持って「大丈夫です!!」と答えております。

それではなぜ、大丈夫なのでしょうか。理由は次の3つの理由からです。
1.図形は最後は計算問題
図形の代表的な問題である「面積」。
こちらは公式を理解すれば、「半径や円周率」や「底辺と高さ」という数字を代入すると、あとは計算問題になってしまいます。
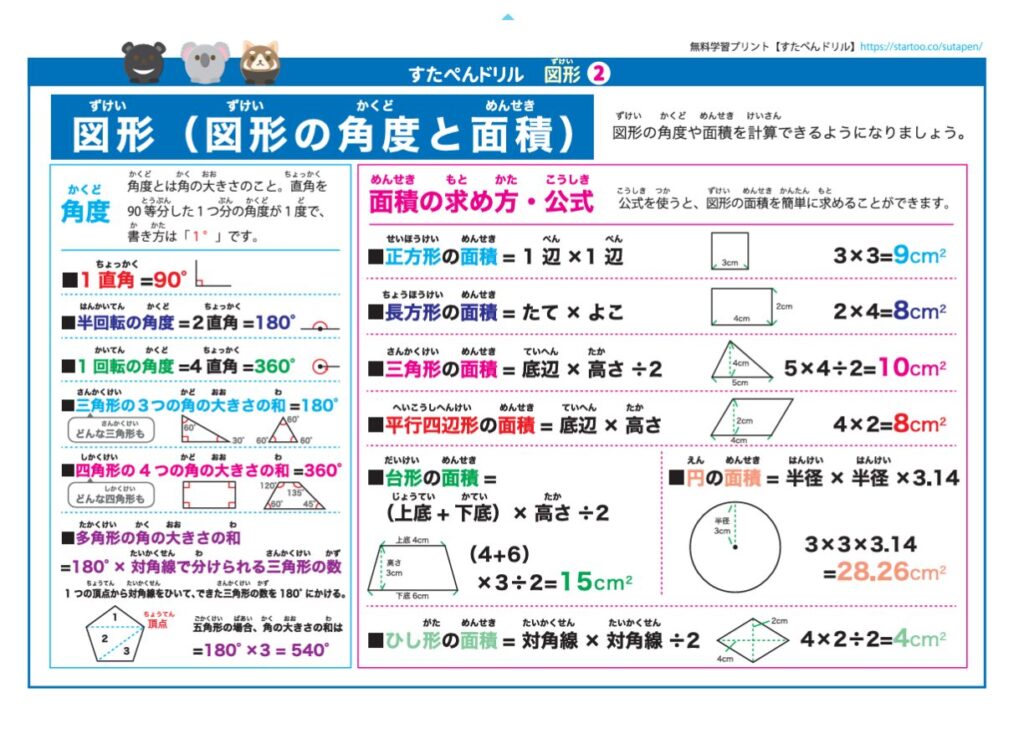
図形が苦手な子の特徴は、
①公式を覚えていない
②使う公式を間違えている
③計算ミス
の3つが原因であることがほとんどです。
それでは公式を覚えるために、何枚も何度もプリントをする必要があると思いますか。
私は不要だと考えます。授業をしっかり聞き、お家で復習すれば、図形の公式は覚えることができると思います。
ここに時間を掛けることはもったいないと思います。

それ以上に数学のメインである計算力を高めるべきだと思います。
また図形は学年が進むにつれて、計算問題色が強くなります。
高校の図形問題は、文字やsin,cos、ベクトルを使った、文字計算問題になります。
小学校では必須だった「コンパス」「分度器」、高校の数学の授業で使った記憶ありますか?
2.文章問題は読解力が必要な計算問題
佐々木さんの家から学校までの道のりは 3.6km、学校から駅までの道のりは3.36km です。ある日、7時15分に家を出て7時35分に学校につきました。その後15時44分に学校を出て16時に駅に着きました。 佐々木さんは、家から学校までと学校から駅までそれぞれ分速何mで移動しましたか。
解答 家から学校:分速180m 学校から駅:分速210m
ここで求められる力は、
①正しく文章を理解する読解力がある
②速さ・時間・距離の計算ルールを使える
③単位を合わせることができる
④正しく計算できる計算力がある
です。
①〜③は算数・数学の力というよりも、国語力と図形同様に公式・ルールを覚えることができることではないでしょうか。
それでは公式・ルールを覚えるために、何枚も何度もプリントをする必要があると思いますか。
私は不要だと考えます。授業をしっかり聞き、お家で復習すれば、公式・ルールは覚えることができると思います。
ここに時間を掛けることはもったいないと思います。

文章問題は学年が進むにつれて、少なくなってきます。
高校入試を境に、数学の問題はかなりシンプルな表現で書かれています。

※解答は割愛いたします
このように「〇〇を求めよ」というシンプルな表現が入試でも使われます。
3.高校数学を見据えると「分数計算力」を高めることが一番重要
高校数学で必要になるのは、「分数計算力」です。
積分の問題です。
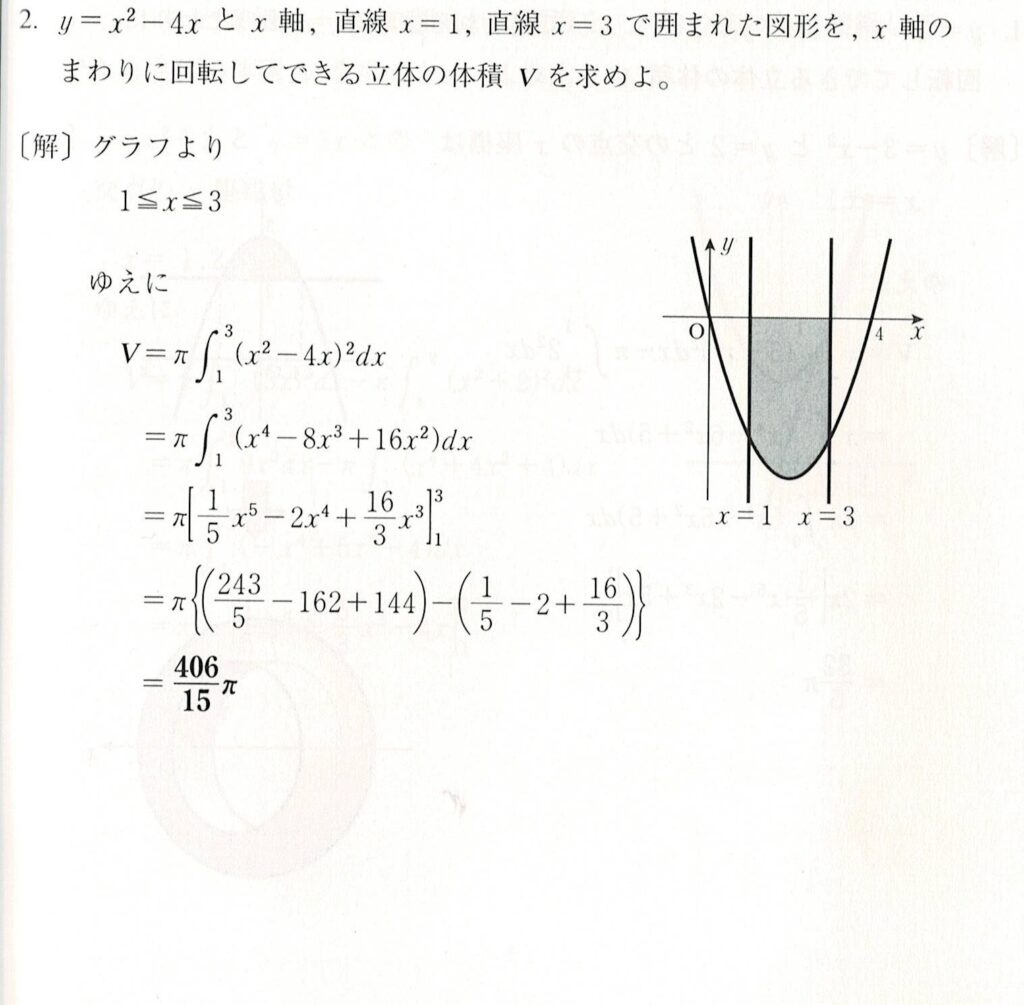
1つの公式を覚えれば、あとは分数計算力しか求められていません。
そのために、あれもこれもしますか?
計算力を高めることに特化したほうが良いと思いませんか。
これが私が図形や文章問題が必要ないとう理由です。
武蔵中原駅 徒歩4分 大戸神社から徒歩30秒
英検合格なら「公文式大戸神社前教室」

